Striking the privacy-utility balance is the central challenge to organizations handling sensitive data. Assessing the privacy side of the balance requires understanding how different privacy policies are undermined. This post will focus on one particular attack against privacy and show how two different privacy policies respond to this attack.
In our context, a privacy-preserving policy is any set of rules, restrictions, or processes which are applied to the data and the data analyst for the purpose of obscuring sensitive data within a database. As an introduction, examples of privacy-preserving policies include:
Future posts will provide more depth about the different privacy-preserving policies, where they are appropriate, and how they could be circumvented. This post will illustrate one specific attack applied to two policies: the aggregate-only policy and differential privacy. We will show how this attack undermines aggregate-only policies and how differential privacy prevents the attack.
The aggregate-only policy is typically developed under the assumption that aggregation provides sufficient anonymity. The misconception is that a kind of “anonymity of crowd” protects the privacy of individual records since no analyst can drill down to any individual record. The one flaw in this assumption, as discussed elsewhere (2), is that a savvy analyst can construct complementary queries to infer the exact values of any record within the database, while still adhering to the restrictions set forth in the aggregate-only policy. In order to further demonstrate these flaws, let’s first lay out what restrictions of a hypothetical aggregate-only policy would be:
Next, consider applying this kind of aggregate only policy to the chronic kidney disease dataset (3), which contains potentially sensitive data about a host of diseases and medical conditions a subject may have. The hypothetical aggregate-only policy shown above would block two classes of queries, examples of which are shown below. The first blocked class of queries directly selects the disease status, either True or False, for a subject, in the example below Subject 247. This would be rejected under the first condition of the aggregate-only policy, where only aggregates can be run. The subqueries of the second class of queries satisfy the aggregate-only condition by using the COUNT(*) aggregate function. However, both would be rejected since, in either case, the COUNT aggregation is evaluated over a group containing a single observation, in violation of the second condition.
So, what is the issue? Under this hypothetical aggregate-only restrictions both queries would be rejected. Subject 247 can sleep safely knowing we have been good stewards of their data, right? Not quite.
Let’s rephrase the second query slightly, and show how trivially the aggregate-only policy’s constraints can be overcome. Rather than filtering the dataset to only Subject 247, we could simply issue two queries. The first would select the entire population (N=400). The second would simply select everyone but Subject 247, leaving 399 records in the subpopulation. By simply subtracting the two counts, we can know Subject 247’s disease status unambiguously.
In this query, we’ve issued only aggregates — satisfying constraint #1 — and run them over sufficiently large populations (N=400 and 399, respectively) — satisfying constraint #2. Using this query we will see the following results:
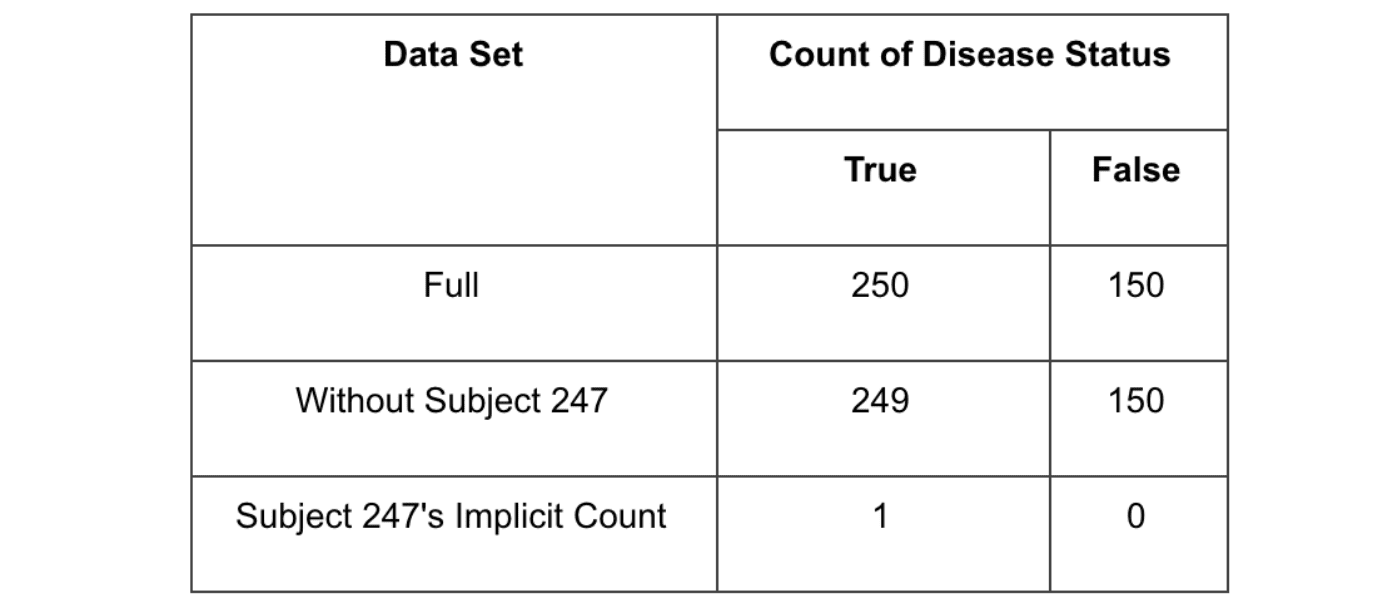
This attack directly undermines the objectives of our aggregate-only policy. We can infer Subject 247’s disease status without ever violating our hypothetical aggregate-only policy.
The query above shows an attack known as a “leave-one-out” attack. Using some prior knowledge uniquely identifying a subject, such as the subject’s birthdate, gender, address, etc., the attacker defines two queries: one query selecting everyone in the database, and a second query selecting everyone who does not match the subject’s attributes. Using simple algebra the attacker can simply compute the subject’s sensitive data.
This kind of attack raises the question: Can we successfully perform an analysis in such a way that it is not possible to work out the contributions of individual subjects?
To protect the contributions of individual data subjects, we need to define a process which makes it difficult to measure the contributions of any single record. Differential Privacy is an example of this kind of process. Differential Privacy makes it difficult to measure the contributions of a single record by adding sufficient randomized noise into the aggregation, such that the contribution of any single record is obscured. Differential Privacy achieves a privacy guarantee. We will discuss the formalities of the differential privacy guarantee in a series of posts in the near future. In rough terms, the guarantee states that for any set of possible outputs, S, of a differentially private query, M, the probability of M returning a value from S is almost equally likely over any pair of databases (D1 and D2) that differ by only one record. The relative probability of observing the event, S, over either database is controlled by the privacy-loss parameter, ϵ. The guarantee is formally expressed below: (4)
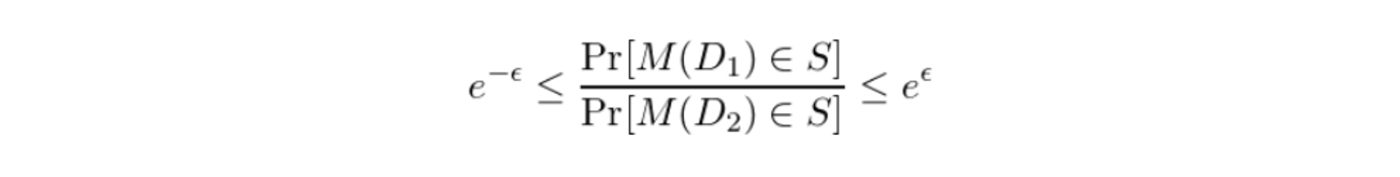
We will delve more deeply into the formalism of differential privacy in later posts.
So how does this help Subject 247? In simple terms, D1 could contain Subject 247’s data, while D2 might not. Regardless, we have some non-zero probability of getting the same query output Meaning that we are not we cannot determine Subject 247’s contribution with certainty. Differential privacy provides this protection to any subject in our database, by adding noise that is sufficiently large so that the contribution of any one record is obscured. As a result, the individual contributions of any record cannot be inferred with certainty. As an example, let’s execute the query above on a table protected by Immuta’s Differential Privacy policy.
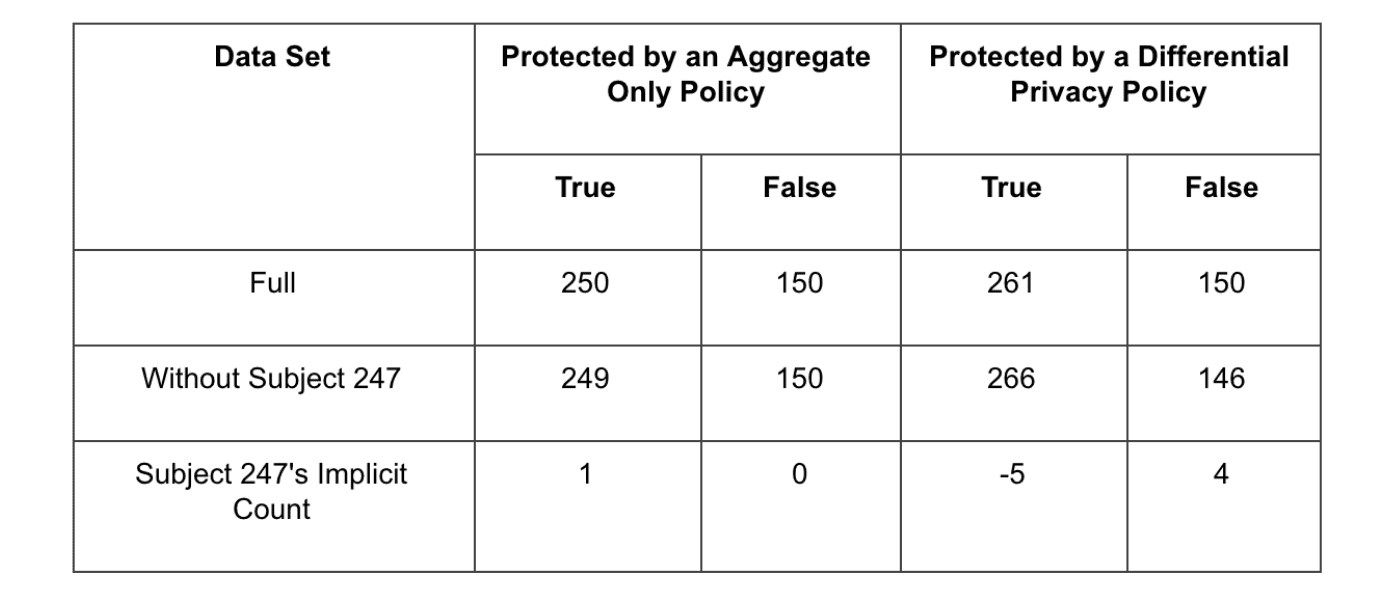
When we attempt to infer Subject 247’s status, we see that there is too much noise to reliably infer their true disease status. At the same time, we’ve sacrificed some accuracy in our analysis, measuring the percentage of subjects with kidney disease as 63.5% under DP while the nominal value is 62.5%. But we’ve paid this price in order to protect our all subjects’ privacy. The privacy-loss parameter, ϵ, controls the amount of noise added to the aggregate, striking a balance between privacy and utility.
We have demonstrated the kind of attack vectors which compliance personnel and data protection officers should consider when developing policies, as well as the impact to utility, seen in this example as a loss of accuracy.
Compliance and privacy personnel, in particular, operate under the burden of understanding how privacy and utility can be measured and balanced. They must assess the accuracy requirements, level of trust of the data consumers, expectations of the data subjects, and potential attack modes meant to circumvent privacy policies. As a result, there isn’t a one-size-fits-all privacy policy that can be applied over all data sources and use cases. Instead, privacy personnel need a rich set of tools which can be applied and adjusted across numerous data sources and use cases.
But differential privacy can be an incredibly important tool in helping to find the right balance, offering a secure alternative to aggregate only policies. In the coming weeks, Immuta will be publishing a series of blogs to help provide privacy and compliance personnel with an overview of the tradeoffs, privacy enhancements, and vulnerabilities of different policy types.
***
Immuta is the only platform to provide differential privacy for the mathematical guarantee of privacy of data sets. Our policy engine is based on plain English, so data governance personnel and data stewards can build complex policies without having to write (or even know) custom code.
Schedule a 1:1 demo to see how Immuta’s platform can help you rapidly personalize data access and dramatically improve the creation, deployment, and auditability of machine learning and AI.
(1) While randomization is not a strict requirement of DP, deterministic methods are of extremely limited utility, as they must necessarily return the same value over all possible inputs.
(2) https://www.ftc.gov/news-events/blogs/techftc/2012/05/aggregate-data-always-private
(3) https://archive.ics.uci.edu/ml/datasets/chronic_kidney_disease
(4) The astute reader may wonder what the greek epsilon refers to. Epsilon can be thought of a parameter which indicates tolerance for privacy loss, and satisfying the above relationship for a small value of epsilon means that the probability distributions of analysis outputs over pairs of adjacent databases must be close in ratio.
