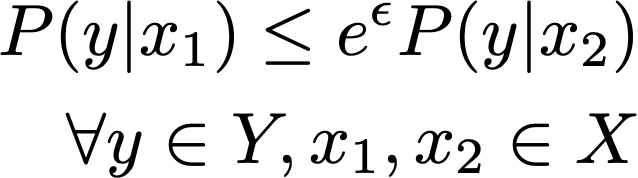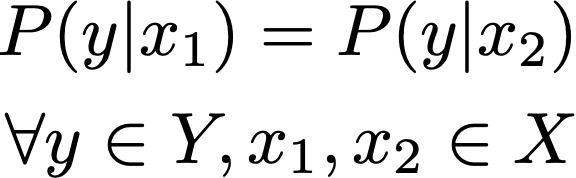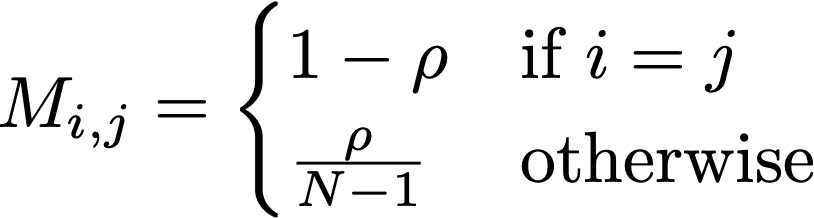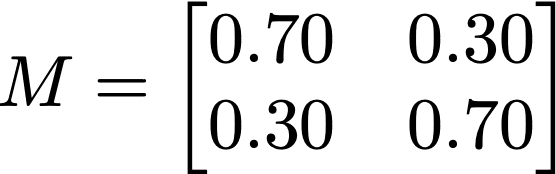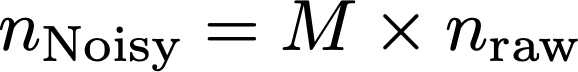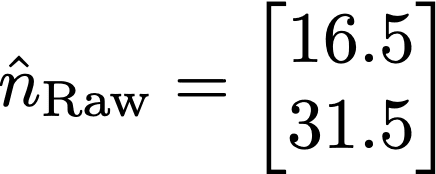Implementing Privacy Controls for Genomics

Genomic data holds significant promise in advancing personalized medicine, streamlining disease treatments, and improving health outcomes. By leveraging individual genetic profiles and biomarkers, genomic data allows researchers to improve treatment accuracy and efficacy. But this promise carries significant privacy risks.

The volume and high dimensionality of genetic data introduces a high risk of subject reidentification, as advanced techniques can link seemingly anonymized genomic information back to specific individuals. The information contained in the genome can reveal latent risks of diseases, genetic disorders, or even predispositions to certain conditions. That knowledge, though important for treatment, may also potentially impact opportunities for fair employment or health insurance, among other things. Additionally, this risk can ripple past a single subject and expand to their current and future relatives.

For instance, one specific risk in this type of sequence data is Single Nucleotide Polymorphism (SNP) barcoding (Oestreich, et. al 2021). SNPs are a genomic variant that occur at a single base pair, and may influence appearance (such as eye color), handedness, disease risk, drug reactions, and many other physical traits and responses. A person can be uniquely identified using between just 30 to 80 SNPs, in a process called SNP barcording. With such a small number of SNPs needed for reidentification, it’s clear why this data is at particular risk of being exploited by attackers.

In this blog, we will discuss particular attack models on SNP data, and how to use Immuta to deploy mitigations, including file access control, row redaction policies, and local differential privacy, to reduce risks from these attacks.

How to Manage VCF Through File Access Control

Genomic data that has gone through alignment and variant calling is often stored in large, compressed VCF files. These files contain samples from a single subject or multiple subjects, as well as information about a single chromosome or multiple chromosomes. The files’ contents make them highly sensitive and risky if they were to fall into a skilled attacker’s hands.

The challenge is how to enable access to these files for legitimate processing purposes, while disabling access for unauthorized users. One option is to broadly limit access to the raw data, only for ingestion purposes and direct analytic operations to structured data environments, such as Snowflake, for all analytic purposes.

Coarse-grained access is a method of access control that entirely limits access to a data set. A hard limit is placed on who and why data can be accessed. While this is a straightforward approach to managing access, it vastly reduces data utility and offers little flexibility.

In contrast, fine-grained access control is a more nuanced approach where data may be obscured, partially redacted, or injected with noise based on numerous factors, including who is requesting the data, the data’s contents, and the purpose for the request. In most applications, fine-grained access control requires the data to be somewhat structured to efficiently apply policies. As a result, coarse-grained access is used to control file ingestion and, once structured, fine-grained controls can be applied.

In this section, we will discuss how Immuta applies coarse-grained controls on file ingestion, supporting the transformation of VCF files into Snowflake tables. This will be followed by sections about how to apply fine-grained controls to structured tables.

Enforcing File Access Control in Amazon S3

Immuta’s native integration with Amazon S3 allows users to centralize permission management on all S3 buckets and limit access to S3 objects. The scale and flexibility of S3 make it a popular landing space for VCF files and other genomic data. As a demonstration, consider an S3 bucket with a collection of VCF files:

If we want to limit access to only HG files, we can define an Immuta data source:

Immuta can control who and why this data can be seen, and enable this data to be staged into Snowflake.

Once created, the user will be given an AWS access key, secret key, and session token. These can be used to expose the data into Snowflake:

-- Access to HG 00110 is allowed
create or replace stage HG00110
	directory = (enable = true)
	url = 's3://bucket/genomics/HG00110.hard-filtered.vcf.gz'
	CREDENTIALS=(AWS_KEY_ID=$aws_key AWS_SECRET_KEY=$aws_secret AWS_TOKEN=$aws_token);

-- Access to HG 00111 is allowed
create or replace stage HG00111
	directory = (enable = true)
	url = 's3://bucket/genomics/HG00111.hard-filtered.vcf.gz'
	CREDENTIALS=(AWS_KEY_ID=$aws_key AWS_SECRET_KEY=$aws_secret AWS_TOKEN=$aws_token);

-- Access to NA 21122 is blocked
create or replace stage NA21122
	directory = (enable = true)
	url = 's3://bucket/genomics/NA21122.hard-filtered.vcf.gz'
	CREDENTIALS=(AWS_KEY_ID=$aws_key AWS_SECRET_KEY=$aws_token);

After running this ingest statements we see:

How to Enable Dynamic Consent Using Immuta

Consent-based authorization for healthcare data access and usage gives individuals the ability to make informed decisions about how their personal health information is used and shared. By obtaining explicit consent from patients or research participants, healthcare organizations increase trust and transparency, while preserving subjects’ privacy and trust.

However, most patients lack the knowledge, confidence, or power to understand complex consent forms and take full agency over how their data is used. The potential to monetize health data – and genomic data in particular – means there is less incentive for companies to adopt consent-based models. As a result, patients may share genomic information for a specific reason, such as genetic testing, and in doing so, they may inadvertently open it up to be shared with other unknown third parties.

In this section, we’ll look at how to shift to a consent-based model using dynamic consent, where a patient can proactively limit how their data is used within clinical and research settings.

A Primer on Health Data Consent Models

Gaining consent to collect, store, and use health data is a prerequisite for any healthcare organization. In doing so, there are two contrasting models for using health data:

1. Broad Consent: This model focuses on maximizing data utility. Individuals consent to their data being used for research purposes, but they may retain little to no control over who the data is shared with or why it is being shared.
2. Dynamic Consent: In this model, an individual retains control over their data and consent, and is able to update their choices over time. They retain the underlying right to control how their data is being used in the future.

Dynamic consent requires research organizations to take a more agile approach to data policy enforcement, one which can quickly respond as subjects update how their data can be used. Although dynamic consent grants more autonomy over data to the data subjects, it requires specific controls and technical capabilities to operationalize effectively.

Threat Model

Consider genetic data collected from a broad patient population. At some point, a subset of these patients ask that their data only be used for colon cancer research. This can either be done by creating special data sets only for colon cancer research, or by dynamically removing those patients from queries which do not cover colon cancer research.

The process of dynamically removing those patients is known as a Row-Level Security or a Row Redaction policy. Implementing a row redaction policy unburdens an analyst from having to track which patients’ data is acceptable to use in different circumstances.

Implementing a Row Redaction Policy

Stuart Ozer, VP of SnowCAT at Snowflake, provides an excellent example of how to use genomics data in Snowflake in his blog. We will use this as a starting point for this analysis.

In this scenario, we’ll load the VCF file data from the 1000 genomes project into a Snowflake table. We’ll follow this example, but increase the samples from 8 to 50:

create or replace table GENOTYPES_BY_SAMPLE (
  CHROM  	varchar,
  POS   	integer,
  ID   	varchar,
  REF   	varchar,
  ALT   	array ,
  QUAL  	integer,
  FILTER 	varchar,
  INFO  	variant,
  SAMPLE_ID  varchar,
  VALS  	variant,
  ALLELE1 	varchar,
  ALLELE2 	varchar,
  FILENAME	varchar
);

insert into GENOTYPES_BY_SAMPLE (
  CHROM  	,
  POS   	,
  ID   	,
  REF   	,
  ALT   	,
  QUAL  	,
  FILTER 	,
  INFO  	,
  SAMPLE_ID  ,
  VALS  	,
  ALLELE1 	,
  ALLELE2 	,
  FILENAME	)
with file_list as (
  SELECT file_url, relative_path FROM DIRECTORY( @dragen_all )
  where relative_path rlike '/HG001[1-7][0-9].*.hard-filtered.vcf.gz' order by random() //temporary hint to maximize parallelism 
)
select
  replace(CHROM, 'chr','')   	,
  POS    	,
  ID    	,
  REF    	,
  split(ALT,','),
  QUAL   	,
  FILTER  	,
  INFO   	,
  SAMPLEID 	,
  SAMPLEVALS	,
  allele1(ref, split(ALT,','), SAMPLEVALS:GT::varchar) as ALLELE1,
  allele2(ref, split(ALT,','), SAMPLEVALS:GT::varchar) as ALLELE2,
  split_part(relative_path, '/',3)
from file_list,
	table(ingest_vcf(BUILD_SCOPED_FILE_URL(@dragen_all, relative_path), 0)) vcf
;

We also created a new support table, MARKERS, matching loci with associated conditions:

CREATE OR REPLACE TABLE markers (
	MARKER_ID varchar,
	CHROM varchar,
	POS number,
	REF varchar,
	clndn varchar
);
INSERT INTO markers
SELECT DISTINCT chrom || '::'|| pos || '::' || ref , chrom, pos, ref, f1.value
FROM clinvar p, lateral flatten(input => p.CLNDN) f1;

Applying Policy

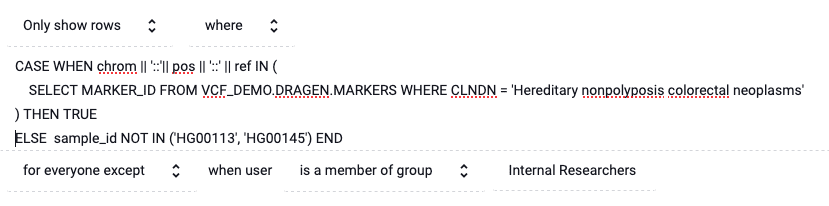
Let’s say a subset of patients associated with sample identifiers HG00113 and HG00145 have asked that, if shared with external researchers, their data only be used for colon cancer research. This requires capturing two circumstances: which data to redact and from whom to redact it.

We can capture which data to redact with the following SQL predicate:

CASE WHEN chrom || '::'|| pos || '::' || ref IN (
SELECT MARKER_ID FROM 
VCF_DEMO.DRAGEN.MARKERS 
WHERE CLNDN = 'Hereditary nonpolyposis colorectal neoplasms'
) THEN TRUE 
ELSE sample_id NOT IN ('HG00113', 'HG00145') END

Rows will only be shown when this predicate is evaluated as True. So, in the case when CLDN is associated with colon cancer, all rows will be shown. Otherwise, only rows where sample_id is not HG00113 or HG00145 will be shown.

Immuta policies are able to include exceptions in order to convey which researchers should see this policy. In this case, we exempt all researchers in the Internal Research group. When applied, the policy will be:

When issuing the following query, both internal and external researchers will see the same data:

select g.chrom, g.pos, g.ref, allele1, allele2, count(1) as allele_count
from genotypes_by_sample g
inner join (
	SELECT chrom, pos, ref FROM markers where
  CLNDN = 'Hereditary nonpolyposis colorectal neoplasms'
) c
on c.chrom = g.chrom and c.pos = g.pos and c.ref = g.ref
GROUP BY 1, 2, 3, 4, 5
ORDER BY COUNT(1) DESC

The policy will be enforced if a user who is not a member of the Internal Research group attempts to access patient records HG00113 or HG00145 for another disease. As an example, let’s tweak the query above to read (note the WHERE sample_id IN (‘HG00113’, ‘HG00145’) clause is included to explicitly show the null result.):

select g.chrom, g.pos, g.ref, allele1, allele2, count(1) as allele_count
from genotypes_by_sample g
inner join (
	SELECT chrom, pos, ref FROM markers where
  CLNDN = 'Retinal dystrophy'
) c
on c.chrom = g.chrom and c.pos = g.pos and c.ref = g.ref
WHERE sample_id IN ('HG00113', 'HG00145')
GROUP BY 1, 2, 3, 4, 5
ORDER BY COUNT(1) DESC;

A member of the internal research would see:

An external researcher, on the other hand, would see an empty set of data:

Using controls of this nature, organizations can smoothly couple up-to-date patient consent with effective clinical practices.

How to Enable Privacy Preserving Data Sharing

Genomic data sharing is a key driver of innovation and translating research into meaningful clinical outcomes. But broad sharing also carries the risk of unnecessarily leaking private information. For healthcare organizations, this could result in losses of patient trust, reputation, and money due to fines.

To counter this, there has been significant work in the field of private data sharing. Two recent publications focus on the use of Local Differential Privacy as a means of sharing genomic data while preserving privacy (Halimi, et. al. 2022 and Yilmaz, et. al, 2022).

Genomic studies are a good use case for Local Differential Privacy (LDP) because:

• Noise can be tuned to meet a study’s utility requirements
• The value domain is finite
• It provides plausible deniability for subjects in the study, since it is unclear whether a disclosed attribute is real or a consequence of a randomizer

Immuta offers a Randomized Response policy which, if the domain is known, follows the definition of LDP. This section will discuss what attacks LDP can be used to counter, and how it can be implemented in Immuta.

Threat Model

The typical threat model breaks the threat to privacy in data sharing along two paths (Bonomi, Huang, and Ohno-Machado 2020):

1. Identification: An attacker uses a portion of genetic information, as well as other open source demographic information, to identify an otherwise unknown individual.
2. Phenotype Inference: An attacker knows the identity of a subject in a data set, and uses their knowledge of that individual’s public attributes to learn some private information, such as genetic markers or disease status. In broader privacy literature, this is referred to as attribute disclosure.

Halimi, et. al. 2022 presents a specific example of phenotype inference involving two roles: a researcher and a verifier. The Researcher is performing a well-intended analysis on a real-world data set. Meanwhile, an external observer, assuming the role of Verifier, attempts to validate the results of the Researcher’s analysis.

The real-world data set may contain a mixture of publicly available, indirect identifiers, such as demographic information, as well as sensitive information, such as disease status and genomic attributes, including Single Nucleotide Polymorphisms (SNPs). Direct identifiers, such as medical record numbers, tax identification numbers, or names will be removed from the data set. Weakly identifying attributes, sometimes called indirect or quasi-identifiers, such as age, sex, or city of residence, will still be present.

The Researcher may detect a strong, but previously unobserved association, between genetic markers and disease status. This association may be real, or the result of computational errors or quality control failures. Regardless, the goal is to enable the Verifier to validate the results.

However, a rogue Verifier could attempt to re-identify a subject or infer their predisposition to a disease. How can the Researcher provide a data set of sufficient quality such that the Verifier can still detect honest computational errors or failures in quality control, without the possibility of learning private information about a patient?

Data Controls

It is useful to think about data privacy controls in the analytics term of Signal-to-Noise Ratio (SNR). In fact, any analytic activity often comes down to discriminating between relevant information (signal) and irrelevant information (noise).

In privacy preserving analytics, we need to place controls on the data such that the signal of personal data is sufficiently obscured, but the signal of some types of non-personal information is still detectable.

As such, privacy controls can be seen as countermeasures that reduce SNR. This can be done by either reducing signal or increasing noise. Typical signal-reducing privacy controls include:

• Suppression: Entirely removing an attribute, typically direct identifiers, from a data set.
• Rounding/Generalization: Replacing a value with a less specific value. For example, bucketing age to the nearest decade (35 years of age is represented by 30-40 years of age).
• K-anonymization: Requiring that each record in a data set be identical to at least k-1 other records. This is the process of hiding in a crowd, so that each individual in a data set appears to be identical to several more members. As a result, it is difficult to single out any one individual. l-Diversity and t-Closeness are variants of K-anonymization. In practice, k-anonymity is achieved through a mixture of suppression and generalization.

On the other side, privacy controls also increase noise in order to obscure low level signals, such as personal information. Examples of noise increasing countermeasures include:

• Randomization: Swapping or applying noise to observations.
• Local Differential Privacy: Scaling noise to limit the bits of information disclosed within an attribute. This is a variant of randomization.
• Global Differential Privacy: Limiting queries using a central aggregator to only allow aggregate-style queries. Noise is added such that the contributions of any potential participant are obscured, so the analyst cannot confidently detect if any potential participant is included in the data set.

The challenge under the threat model described earlier is that the disclosed data set must have sufficiently high SNR that computational or quality errors can be detected, but sufficiently small that individual attributes cannot be confidently inferred. As such, the SNR produced by privacy controls needs to be closely monitored.

Local Differential Privacy Definition

Differential privacy is a family of mathematical techniques that formally limit the amount of private information that can be inferred about each data subject, and hence are desirable properties of privacy mechanisms.

There are two main types of differential privacy, offering slightly different privacy guarantees:

1. Global Differential Privacy, which offers data subjects deniability of participation
2. Local Differential Privacy, which offers deniability of record content.

Despite being slightly different formal models of privacy, both operate by introducing randomization into data computations to prevent an attacker from reasoning about its subjects with certainty. Ultimately, these techniques afford data subjects deniability while still allowing analysts to learn from the data.

Local differential privacy is of particular relevance in guarding against the Verifier attack model. Consider an attacker who wishes to make inferences regarding a data subject’s private or sensitive information. If such data is simply present in a database table or query result, the adversary will learn the sensitive value with absolute certainty.

Alternatively, consider a process that randomizes the values instead of returning them in the clear. Such a process could flip a biased coin, returning the actual value whenever the flip comes up as heads. But, when the flip comes up as tails, the data value – let’s say the presence of a given SNP – is replaced or reversed. The adversary cannot know the outcome of the coin flip, only the final resulting value.

Such a process has the obvious benefit that an adversary is unable to be certain about the truth or accuracy of the observed values. This affords data subject deniability because the observed value could be the effect of the randomizer instead of the true content of the subject’s record. Moreover, since the randomizer behavior in the above example follows a well-defined noise model, it can often be corrected. This allows for fairly accurate count operations over randomized values.

A randomization mechanism, in which a randomized output y is produced as a consequence of an input value x, is considered locally differentially private if the following definition is satisfied:

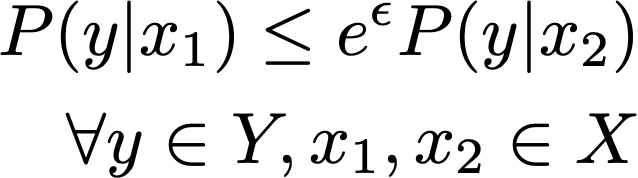
This expression requires that the probability of observing any disclosed value y given an input value x₁ is bounded above by observing y given another input x₂. This definition must hold for any pair of outcomes over the domain of X for all potential outcomes over the domain of Y. The upper bound is scaled by e^ϵ where ϵ must be non-negative. The upper bound scales to how close the two probabilities must be.

In the extreme case, if ϵ = 0, the above expression effectively becomes:

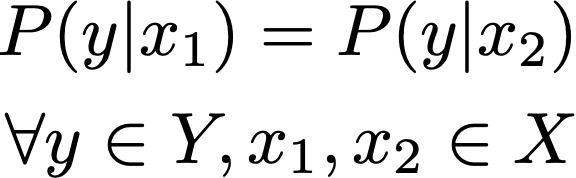
Any outcome y is equally probable given between any pair of inputs, x₁ and x₂. This case reflects complete anonymity, and consequently no utility. As ϵ increases, the resulting probability distributions can start to diverge, meaning that the analytic value of observing y increases.

Example

Let’s consider the example of SNP rs199512, which has been associated with handedness. To study this SNP, we create the following table in Snowflake:

CREATE TABLE rs199512 (
	filename string,
	sample_id string,
	chrom string,
	pos number,
	ref string,
	allele1 string
);
insert into rs199512
SELECT filename, sample_id, chrom, pos, ref, allele1 
FROM genotypes_by_sample
WHERE chrom = '17' AND pos = 46779986
ORDER BY sample_id;

We want to limit the verifier’s ability to observe the unperturbed data. To this end, we will define the following randomized response policy:

This policy will randomize approximately 30% of the rows of the allele1 attribute by flipping T to C or vice versa. The result will effectively flatten the distribution to something more uniform, meaning the verifier will not be confident that the result is due to randomization versus the true allele value.

Once applied, the researcher will still be able to see the true value, while the verifier will see a noisy version of the data. If we run the following query:

SELECT allele1, COUNT(1)
FROM rs199512
GROUP BY 1;

The following counts will be returned:

Allele	Researcher Counts (Raw)	Verifier Counts (Noisy)
T	17	21
C	31	27

It is noted in Halimi, et. al., that the impact of randomization on the distance between the raw and noisy data sets is independent of the phenotype being studied. As a result, a well understood reference sample can be used to validate the results from a noisy data set.

Another interesting aspect of randomization is that it can be represented using a Markov matrix. Generally this takes on the form:

In this expression, N are the size of the randomized attribute’s domain, and ρ is the replacement rate. In the case of this allele, N is taken as 2, and ρ = 0.30. In case of rs199512, this matrix takes on the form:

We can represent the noised counts using the following linear equation:

Where n_Noisy and n_raw are the noisy and raw counts, respectively. Now, the verifier only observes the noisy counts, but can make an estimate of the raw counts by solving this equation for n_raw. This can be done in Python using numpy, in R using Solve, or MATLAB using the backslash operator, provided the matrix is well conditioned. If the verifier is given access to the randomization rate, they will know M, and can solve for n_raw. Using numpy, results in an estimate of n_raw of:

Conclusion

The stakes for accessing and sharing genomic data have never been higher. And yet, the processes for doing so are not well defined.

While EU-based regulators grant data subjects ownership over their data in perpetuity, US-based healthcare systems take a more black-and-white approach; genomic information that an individual shares with a single company for a single purpose may be transferred to third parties and so it can be monetized beyond the original intent. Not only does this pose a substantial security risk, but it also violates data subjects’ privacy. Left unchecked, this will have long-lasting implications on individuals for generations to come.

To avoid the immediate and long term implications of this scenario, now is the time to adopt dynamic consent-based authorization models. Historically, the compute resources to handle dynamic consent requirements did not exist. Today, tabular storage approaches and scalable compute infrastructure make it possible. With the right tools and capabilities – including fine-grained access controls, row redaction policies, and privacy-enhancing technologies like k-anonymization and randomized response – this outcome isn’t just attainable; it’s easily within reach.

Ultimately, this shift will allow governance teams and regulators to de-risk data so researchers can securely and freely do more with it. It’s a change that will benefit not just healthcare companies but patients, providers, and the industry as a whole.

References

• Bonomi, Luca, Yingxiang Huang, and Lucila Ohno-Machado. 2020. “Privacy Challenges and Research Opportunities for Genomic Data Sharing.” Nature Genetics 52 (7): 646–54.
• Oestreich M, Chen D, Schultze JL, Fritz M, Becker M. Privacy considerations for sharing genomics data. EXCLI J. 2021 Jul 16;20:1243-1260. doi: 10.17179/excli2021-4002. PMID: 34345236; PMCID: PMC8326502.
• National Institutes of Health. 2014. “NIH Genomic Data Sharing Policy”. https://grants.nih.gov/grants/guide/notice-files/NOT-OD-14-124.html
• Halimi, Anisa, Leonard Dervishi, Erman Ayday, Apostolos Pyrgelis, Juan Ramón Troncoso-Pastoriza, Jean-Pierre Hubaux, Xiaoqian Jiang, and Jaideep Vaidya. “Privacy-preserving and efficient verification of the outcome in genome-wide association studies.” In Proceedings on Privacy Enhancing Technologies. Privacy Enhancing Technologies Symposium, vol. 2022, no. 3, p. 732. NIH Public Access, 2022.
• Yilmaz, Emre, Tianxi Ji, Erman Ayday, and Pan Li. “Genomic data sharing under dependent local differential privacy.” In Proceedings of the twelfth ACM conference on data and application security and privacy, pp. 77-88. 2022.